Exercise 13
1. ধৰা a ∝ b। যেতিয়া b = 21, a = 7, হয়; যদি a = 2, তেন্তে b ৰ মান কি?
Solution:-
দিয়া আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 7, b_1 = 21\) আৰু \(a_2 = 2, b_2 = x\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{7}{21}\) = \(\frac{2}{x}\)
\(7x = 2 × 21\)
\(x = \frac{2× 21}{7}\)
\(x = 2×3\) = 6
2. চেনিৰ মূল্য প্রতি কিলোগ্ৰামত 30 টকা। 12 কিলোগ্ৰামৰ দাম উলিওৱা। 165 টকাত কেই কিলোগ্রাম চেনি পোৱা যাব?
Solution:-
ধৰো, চেনীৰ মূল্য = \(a\)
চেনীৰ পৰিমাণ = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে চেনীৰ মূল্য আৰু চেনীৰ পৰিমাণ প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 30, b_1 = 1\) আৰু \(a_2 = x, b_2 = 12\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{30}{1}\) = \(\frac{x}{12}\)
\(x=12×30x=12×30\)
\(x=360\)
আকৌ, ধৰো,
\(a_1 = 30, b_1 = 1\) আৰু \(a_2 = 165, b_2 = x\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{30}{1}\) = \(\frac{165}{x}\)
\(30x = 165\)
\(x = \frac{165}{30}\)
\(x = \frac{165}{30}\) = 5.33
3. এটা আয়তৰ কালি 60 বৰ্গ মিটাৰ। সমানুপাত প্রয়োগ কৰি ইয়াৰ প্ৰস্থ উলিওৱা যদি দীঘ = 15 মিটাৰ আৰু দীঘ উলিওৱা যদি প্ৰস্থ = 6 মিটাৰ৷
Solution:-
ধৰো, দীঘ = \(a\)
প্ৰস্থ = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে দীঘ আৰু প্ৰস্থ পৰিমাণ ব্যস্ত সমানুপাতত আছে,
\(a ∝ {1}{b}\)
\(ab = k\)———(I)
ধৰো,
\(a=15 \) আৰু \(ab = 60\)
\(ab\) ৰ মান (i) ত বহুৱাই পাঁও
k = 60
(i) ৰ পৰা
\(ab = k\)
\(15b = 60\)
b = 4
আকৌ,
ধৰো,
\(b=6 \) আৰু \(ab = 60\)
\(ab\) ৰ মান (i) ত বহুৱাই পাঁও
k = 60
(i) ৰ পৰা
\(ab = k\)
\(6a = 60\)
\(a = 10\)
4. 9টা বেলুনৰ দাম 36 টকা। তেনে 14টা বেলুনৰ দাম কিমান ?
Solution:-
ধৰো,
বেলুনৰ দাম = \(a\)
বেলুনৰ সংখ্যা = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে বেলুনৰ দাম আৰু সংখ্যা প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 36, b_1 = 9\) আৰু \(a_2 = x, b_2 = 14\)
\(\frac{36}{9}\) = \(\frac{x}{14}\)
\(\frac{36×14}{9}\) = \(x\)
\(x= 4×14=56\)
5. এটা ঔষধৰ কাৰণে প্ৰতি 2 ভাগ আয় ডিনৰ লগত 6 ভাগ এচিড মিহলোৱা আছে। গতিকে কিমান ভাগ আয়’ডিনৰ লগত কিমান ভাগ এচিড মিহলাব লাগিব তাকে দেখুৱাই তলৰ তালিকাখন পূৰোৱা ।

Solution:-
ধৰো,
আয়ডিনৰ পৰিমাণ = \(a\)
এচিডৰ পৰিমাণ = \(b\)
দিয়া আছে,
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে আয়ডিনৰ পৰিমাণ আৰু এচিডৰ পৰিমাণ প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
(i) ধৰো,
\(a_1 = 2, b_1 = 6\) আৰু \(a_2 = 5, b_2 = x\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{2}{6}\) = \(\frac{5}{x}\)
\(2x = 5× 6\)
\(x = \frac{30}{2}\)
\(x = 15\)
(ii) ধৰো,
\(a_1 = 2, b_1 = 6\) আৰু \(a_2 = 7, b_2 = x\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{2}{6}\) = \(\frac{7}{x}\)
\(2x = 7× 6\)
\(x = \frac{42}{2}\)
\(x = 21\)
(iii) ধৰো,
\(a_1 = 2, b_1 = 6\) আৰু \(a_2 = x, b_2 = 18\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{2}{6}\) = \(\frac{x}{18}\)
\(2× 18 = 6x\)
\(x = \frac{2× 18}{6}\)
\(x = 6\)
(iii) ধৰো,
\(a_1 = 2, b_1 = 6\) আৰু \(a_2 = x, b_2 = 25\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{2}{6}\) = \(\frac{x}{25}\)
\(2× 25 = 6x\)
\(x = \frac{2× 25}{6}\)
\(x = \frac{25}{3}\)
6. এখন ৰেলগাড়ী 4 ঘণ্টাত 240 কিঃমিঃ পথ অতিক্ৰম কৰে। 840 কিঃমিঃ যাবলৈ গাড়ীখনৰ কিমান সময় লগিব?
Solution:- ধৰো,
ৰেলগাড়ীখনে অতিক্ৰম কৰা সময় = \(a\)
ৰেলগাড়ীখনে অতিক্ৰম কৰা দূৰত্ব = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে ৰেলগাড়ীখনে অতিক্ৰম কৰা সময় আৰু দূৰত্ব প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 4, b_1 = 240\) আৰু \(a_2 = x, b_2 = 840\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{4}{240}\) = \(\frac{x}{840}\)
\(4 × 840 = 240x\)
\(x = \frac{4 × 840 }{240}\)
\(x = \frac{84}{6}\) = 14
7. ওপৰৰ প্ৰশ্নত দ্ৰুতি একে থাকিলে গাড়ীখনে 11 ঘণ্টাত কিমান দূৰত্ব অতিক্ৰম কৰিব?
Solution:- প্ৰশ্নটো হব এনেধৰণৰ
এখন ৰেলগাড়ী 4 ঘণ্টাত 240 কিঃমিঃ পথ অতিক্ৰম কৰে। 11 ঘন্টাত গাড়ীখনে কিমান দূৰত্ব অতিক্ৰম কৰিব ?
ধৰো,
ৰেলগাড়ীখনে অতিক্ৰম কৰা সময় = \(a\)
ৰেলগাড়ীখনে অতিক্ৰম কৰা দূৰত্ব = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে ৰেলগাড়ীখনে অতিক্ৰম কৰা সময় আৰু দূৰত্ব প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 4, b_1 = 240\) আৰু \(a_2 = 11, b_2 = x\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{4}{240}\) = \(\frac{11}{x}\)
\(4 × x = 240× 11\)
\(x = \frac{240× 11 }{4}\)
\(x = 60× 11\) = 660
৪. OH খুঁটিটোৰ দৈৰ্ঘ্য 1⁄2 মিটাৰ। খুঁটিটোৰ মাটিত OA ছাঁ = x মিটাৰ। যেতিয়া খুঁটিটোৰ উচ্চতা 10.8 মিটাৰ তেতিয়া ইয়াৰ ছাঁ পোৱা গ’ল 6 মিটাৰ।
(i) যেতিয়া উচ্চতা 8.10 মিটাৰ ইয়াৰ ছাঁৰ দৈৰ্ঘ্য কিমান?
(ii) যেতিয়া ছাঁৰ দৈৰ্ঘ্য 3 মিটাৰ খুঁটি এটাৰ উচ্চতা কিমান হ’ব?
Solution:-
ধৰো, খুটাটোৰ দৈৰ্ঘ্য = \(h\)
খুটাটোৰ ছাঁ = \(x\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে খুটাটোৰ দৈৰ্ঘ্য আৰু ছাঁ প্ৰত্যেক্ষ সমানুপাতত আছে,
\(h ∝ x\)
\(h = kx\)
\(\frac{h}{x}= k\)
(i) ধৰো,
\(h_1 = 10.8, x_1 = 6\) আৰু \(h_2 = 8.10, x_2 = a\)
\(\frac{h_1}{x_1}\) = \(\frac{h_2}{x_2}\)
\(\frac{10.8}{6}\) = \(\frac{8.10}{a}\)
\(10.8a=6×8.10\)
\(a=\frac{6×8.10}{10.8}\)
\(a= 4.5 \)
(ii) ধৰো,
\(h_1 = 10.8, x_1 = 6\) আৰু \(h_2 = a, x_2 = 3\)
\(\frac{h_1}{x_1}\) = \(\frac{h_2}{x_2}\)
\(\frac{10.8}{6}\) = \(\frac{a}{3}\)
\(10.8×3=6a\)
\(a=\frac{3 × 10.8}{6}\)
\(a= 5.4\)
9. যদি x, y, P, q ৰাশি চাৰিটা সমানুপাতত থাকে, দেখুওৱা যে—
\(p =\frac{xq}{y}\) , \(q =\frac{yp}{x}\)
Solution:-
দিয়া আছে, \(x:y::p:q\)
\(\frac{x}{y} =\frac{p}{q}\)
\(p =\frac{xq}{y}\)
আৰু,
\(\frac{x}{y} =\frac{p}{q}\)
\(q =\frac{yp}{x}\)
10. ধৰা দুজন ল’ৰাই 30 ঘণ্টাত বাগিছা এখনৰ বেৰ নিৰ্মাণ কৰিব পাৰে। তেন্তে 10 জন ল’ৰাই সেই বেৰখন কিমান সময়ত নিৰ্মাণ কৰিব?
Solution:-
ধৰো, লৰাৰ সংখ্যা = \(a\)
সময় = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে লৰাৰ সংখ্যা আৰু সময় ব্যস্ত সমানুপাতত আছে,
\(a ∝ \frac{1}{b}\)
\(ab = k\)
ধৰো,
\(a_1 = 2, b_1 = 30\) আৰু \(a_2 = 10, b_2 = x\)
\(a_1b_1\) = \(a_1b_2\)
\(2×30 =10 × x \)
\(x=\frac{2×30}{10}= 2×3 = 6\)
12. এজন স্থপতিবিদৰ এখন মানচিত্ৰৰ স্কেল 1 : 2000 । যদি প্রকৃতভাবে মাটিত সজা ঘৰ এটাৰ দীঘ 1200 ফুট তেন্তে মানচিত্ৰত ঘৰটোৰ দীঘ কিমান ?
Solution:-
ধৰো,
মানচিত্ৰৰ মাপ = \(a\)
প্ৰকৃত মাপ = \(b\)
দিয়া আছে,
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে মানচিত্ৰ মাপ আৰু প্ৰকৃত মাপ প্ৰত্যেক্ষ সমানুপাতত আছে,
\(a ∝ b\)
\(a = kb\)
\(\frac{a}{b}= k\)
ধৰো,
\(a_1 = 2, b_1 = 2000\) আৰু \(a_2 = x, b_2 = 1200\)
\(\frac{a_1}{b_1}\) = \(\frac{a_2}{b_2}\)
\(\frac{1}{2000}\) = \(\frac{x}{1200}\)
\(\frac{1}{2000}\) × 1200 = \(x\)
\(\frac{1200}{2000}\) = \(x\)
\(\frac{12}{20}\) = \(x\)
\(x\) = \(0.6\)
13. এটা আশ্রয় শিবিৰত 387 জন শৰণাৰ্থীৰ 15 দিনৰ খাদ্য মজুত আছিল। যদি শৰণাৰ্থীৰ সংখ্যা 645 জন হয়, তেন্তে এই একেখিনি খাদ্য কিমান দিন খাব পাৰিব?
Solution:-
ধৰো, লৰাৰ সংখ্যা = \(a\)
সময় = \(b\)
প্ৰশ্নৰ পৰা গম পোৱা গৈছে যে শৰণাৰ্থীৰ সংখ্যা আৰু দিনৰ সংখ্যা ব্যস্ত সমানুপাতত আছে,
\(a ∝ \frac{1}{b}\)
\(ab = k\)
ধৰো,
\(a_1 = 387, b_1 = 15\) আৰু \(a_2 = 645, b_2 = x\)
\(a_1b_1\) = \(a_1b_2\)
\(387×15 =645 × x \)
\(x=\frac{387×15}{645}= 9\)
14. শাৰীৰিক শক্তিৰ ক্ষেত্ৰত যদি 20 টা ম’হ 6 টা ঘোঁৰাৰ সমতুল্য; আৰু 5 টা ম’হ 3 টা ষাঁড়গৰুৰ সমতুল্য তেন্তে 10 টা ঘোঁৰা কেইটা ষাঁড়গৰুৰ সমতুল্য ? (ইংগিত : তালিকাত দেখুওৱা ধৰণে x, y সমতুল্যবোৰ বহুৱাই লোৱা। প্ৰত্যক্ষ সমানুপাত প্রয়োগ কৰি x, y ৰ মান উলিওৱা ।)
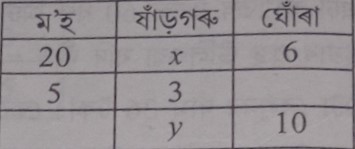
Solution:- তালিকাৰ পৰা দেখা পোৱা গৈছে যে —-
শাৰীৰিক শক্তিৰ ক্ষেত্ৰত মহ , খাড়গৰু আৰু ঘোঁৰা প্ৰত্যক্ষ সমানুপাতত আছে
\(20 ∝ x\)
\(20 = kx\)
\(\frac{20}{x}= k\)———————- (i)
\(5∝ 3\)
\(5 = 3k\)
\(\frac{5}{3}= k\)
k ৰ মান (i) ত বহুৱাই
\(\frac{20}{x}\)=\(\frac{5}{3}\)
\(60 = 5x\)
\(x = \frac{60}{5}\) = 12
আকৌ,
\(y∝ 10\)
\(y = 10k\)
\(\frac{y}{10}= k\)———————- (ii)
\(x∝ 6\)
\(12 = 6k\)
\(\frac{12}{6}= k\)
\(\frac{12}{6}\)=\(\frac{y}{10}\)
\(2*10\)=\(y\)
\(y = 20\)
