Exercise 8.1
1. ABC ত্ৰিভুজৰ B কোণ সমকোণ আৰু AB = 24cm, BC=7cm হ’লে তলত দিয়াবিলাক উলিওৱা
(i) sinA,cosA (ii) sinC, CosC

সমাধান,
দিয়া আছে: AB = 24 cm, BC = 7cm, ∠B = 90°
∴ AC² = AB² + BC² (পিথাগোৰাচৰ সূত্রমতে)
⇒ AC² = (24)² + (7)²
⇒ AC² = 576 + 49 = 625
⇒ AC = 25 cm
(i) sinA = \(\frac{ BC}{AC}\)= \(\frac{ 7}{25}\)
COSA = \(\frac{ AB}{AC}\)= \(\frac{ 24}{25}\)
(Ii) sinC = \(\frac{ AB}{AC}\)= \(\frac{ 24}{25}\)
CosC = \(\frac{ BC}{AC}\)= \(\frac{ 7}{25}\)
2. চিত্র 8.13 ৰ পৰা tanP – cotR নিৰ্ণয় কৰা।
সমাধানঃ- PR = 13cm, PQ = 12 cm
∴ PR² = PQ² + QR²
⇒ (23)² = (12)² + (QR)²
⇒ QR² = 169 – 144 = 25
⇒ QR = 5
∴ tan P = \(\frac{RQ}{QP}\) = \(\frac{5}{12}\)
∴ cot R =\(\frac{RQ}{QP}\) = \(\frac{5}{12}\)
∴ tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0
3. যদি sinA = 3/4, তেন্তে cosA আৰু tanA উলিওৱা।

সমাধানঃ-
ABC এটা সমকোণী ত্রিভুজ। ∠B = 90°
∴ sin A = \(\frac{3}{4}\) = \(\frac{BC}{AC}\) = k ধৰা হ’ল। [সমানতাৰ ধ্ৰুৱক]
∴ BC = 3k, AC = 4k
∴ AC² = AB² + BC² (পিথাগোৰাচৰ সূত্রমতে)
⇒ (4k)² = AB² + (3k)²
⇒ 16k² – 9k² = AB²
⇒ AB² = 7k²
⇒ AB = \(\sqrt7\)k
∴ tan A = \(\frac{BC}{AB}\) = \(\frac{3K}{\sqrt7k}\) = \(\frac{3}{\sqrt7}\)
∴ cos A =\(\frac{AB}{AC}\) = \(\frac{\sqrt7k}{4k}\) = \(\frac{\sqrt7}{4}\)
4. দিয়া আছে যে, 15 cotA = 8, তেন্তে sinA আৰু secA উলিওৱা।
উত্তৰঃ
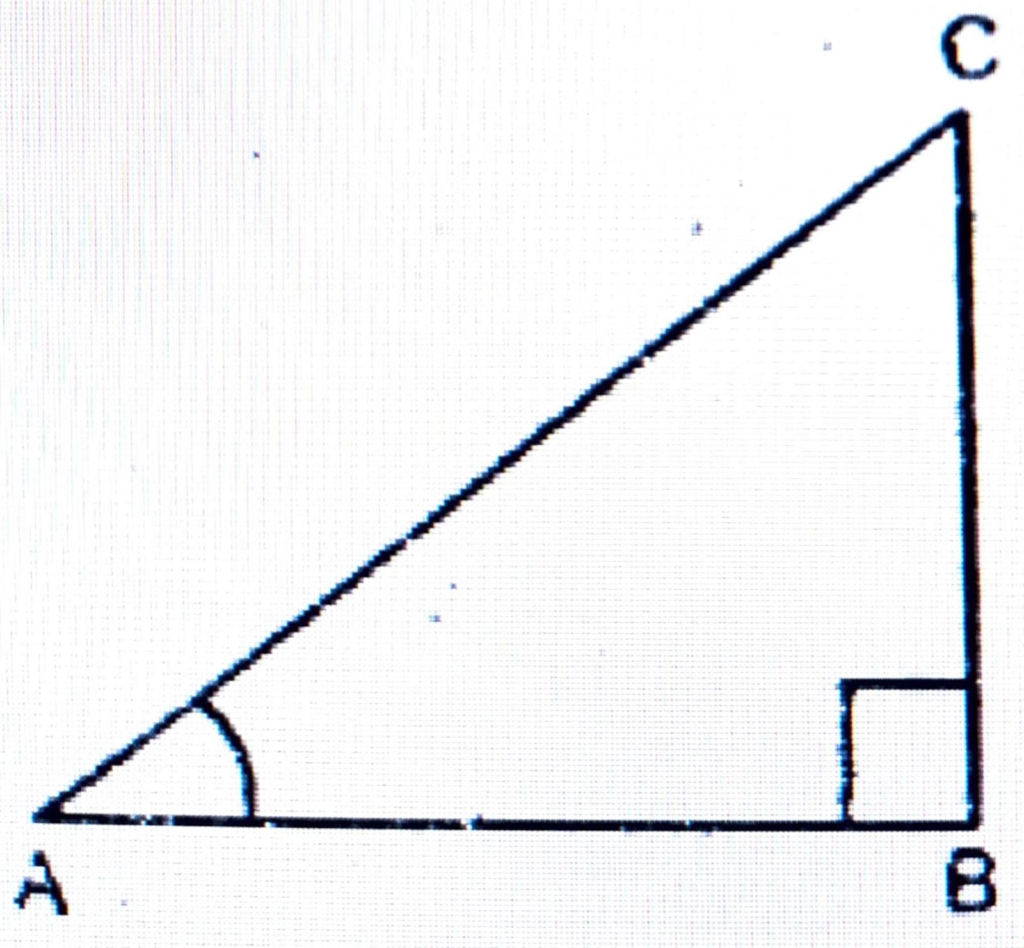
ABC এটা সমকোণী ত্রিভুজ। ∠B = 90°
∴ 15 cot A = 8
⇒ cost A = \(\frac{8}{15}\) = \(\frac{AB}{BC}\) = k ধৰা হ’ল।
∴ AB = 8k, BC = 15k
∴ AC² = AB² + BC²
⇒ AC² = (8k)² + (15k)²
⇒ AC² = 64k² + 225k²
⇒ AC² = 289k²
⇒ AC = 17k
∴ cos A = \(\frac{BC}{AC}\) = \(\frac{15K}{17k}\) = \(\frac{15}{17}\)
∴ sec A =\(\frac{AC}{AB}\) = \(\frac{17k}{8k}\) = \(\frac{17}{8}\)
5. দিয়া আছে যে, secθ = 13/12, আন ত্রিকোণমিতিক অনুপাতবোৰ গণনা কৰা।
সমাধানঃ-

ABC এটা সমকোণী ত্রিভুজ ∠B = 90°, ∠ABC = θ (সূক্ষ্মকোণ)
⇒ secθ = \(\frac{13}{12}\) = \(\frac{AC}{AB}\) = k ধৰা হ’ল। এটা [ধ্রুৱক]
∴ AC = 13k, AB = 12k
∴ AC² = AB² + BC²
⇒ (13k)² = (12k)² + BC²
⇒ 169k² = 144k² + BC²
⇒ BC² = 169k² – 144k²
⇒ BC² = 25k²
⇒ BC = 5k
∴ cos θ = \(\frac{BC}{AC}\) = \(\frac{15K}{17k}\) = \(\frac{15}{17}\)
∴ sec A =\(\frac{AC}{AB}\) = \(\frac{17k}{8k}\) = \(\frac{17}{8}\)
6. যদি ∠A আৰু ∠B সূক্ষ্মকোণ হয় যাতে cosA = cosB, তেন্তে দেখুওৱা যে ∠A = ∠B.
সমাধানঃ- ধৰো ∆ABC ৰ ∠C = 90°
এতিয়া, cos A = \(\frac{AB}{AC}\)
আৰু cos B = \(\frac{BC}{AC}\)
প্রশ্নমতে cos A = cos B
⇒ \(\frac{AB}{AC}\) = \(\frac{BC}{AC}\)
⇒ AB = AC
∴ ABC এটা সমদ্বিবাহু ত্রিভূজ আৰু সমদ্বিবাহু ত্রিভূজৰ
সমান বাহু দুটাৰ বিপৰীত কোণ দুটা সমান
∴ প্রমাণিত হ’ল যে ∠A = ∠B
7. যদি cotθ = \(\frac{7}{8}\) , তেন্তে মান উলিওৱা।
(i) \(\frac{(1 + sin θ) (1 – sin θ)}{(1 + cos θ) (1 – cos θ)}\)
সমাধানঃ-
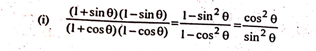
(ii) cot² θ
সমাধানঃ-
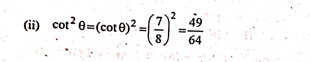
৪. যদি 3 cotA = 4, তেন্তে 1 – tan² A/1 + tan² A = cos² A – sin² A হ’বনে নহয় পৰীক্ষা কৰা।
উত্তৰঃ-


(i) sinA cosC + cosA sinC

10. ∆PQR ৰ Q কোণ সমকোণ আৰু PR + QR = 25cm আৰু PQ = 5cm. sinP, cosP আৰু tanP ৰ মান উলিওৱা।
PQR এটা সমকোণী ত্রিভুজৰ। ∠θ = 90° আৰু ∠P → সূক্ষ্মকোণ।

PR + QR = 25cm আৰু PQ = 5cm.
∴ QR এটা সমকোণী ত্রিভূজৰ পৰা পাওঁ–
PR² = QR² + PQ²
⇒ PR² = (25 – PR)² + (5)²
⇒ PR² = 625 – 50PR + PR² + 25
⇒ PR² – PR² = 650 – 50PR
⇒ 0 = 650 – 50PR
⇒ 50PR = 650
⇒ PR = \(\frac{650}{50}\) = 13cm.
∴ QR = 25 – PR = 25 – 13 = 12cm

11. তলত দিয়াবিলাক সত্য নে অসত্য কোৱা। তোমাৰ উত্তৰৰ যথার্থতা উল্লেখ কৰা।
(i) tanA ৰ মান সদায় 1 তকৈ সৰু।
উত্তৰঃ অসত্য।
(ii) A কোণৰ কোনো মানৰ বাবে secA = 12/5
উত্তৰঃ সত্য।
(iii) ‘cosecant of angle A’ ৰ সংক্ষিপ্ত ৰূপ হিচাপে cosA ব্যৱহাৰ কৰা হয়।
উত্তৰঃ অসত্য।
(iv) cot আৰু A ৰ পূৰণফল হ’ল cotA.
উত্তৰঃ অসত্য।
(v) কোনো এটা কোণ ‘θ’ ৰ বাবে sinθ = 4/3
উত্তৰঃ অসত্য।
