Solution:- ধৰো, m = 5

n = 3

\(m^2 – n^2\) = \(5^2 – 3^2\) = 25 – 9 = 16 যুগ্ম

Ans:- option (a)

Solution:- Option d

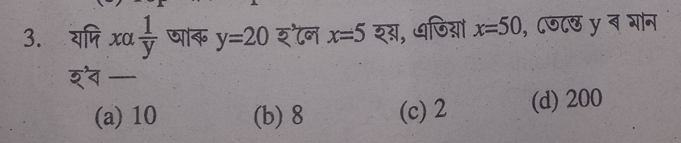
Solution :- দিয়া আছে, \(y_1 = 20\) , \(x_1 = 5\)

\(y_2 = y \) , \(x_2 = 50\)

\(x_1× y_1\) = \(x_1× y_1\)

100 = 50y

y = 2

Option (C)

Solution:-

আমি জানো যে, α + β = b

αβ = k

3α + 2β = 20

ধৰো, α = 8 β = -2

3(8) + 2(-2) = 24 -4 =20

So, αβ = k

8 × -2 =k

-16 = k

Ans:- Option (A)

Solution:-

আমি জানো যে, α + β = – \(\frac{6}{a}\)

αβ = \(\frac{c}{a}\)

A/Q

α + β = αβ

– \(\frac{6}{a}\) = \(\frac{c}{a}\)

C = -6

সমীকৰণটোৰ পৰা পাও যে, b = 6

= b + c

= 6 – 6 = 0

Ans:- Option (b)

Solution:-

3ax + 4y = -2

3(-3)a + 4(4) = -2

= -9a + 16 = -2

= -9a = -18

= a = 2

and, 2x + by = 14

2 (-3) + b (4) = 14

= – 6 + 4b =14

= 4b = 20

= b = 5

Ans:- Option (A)

Solution:-

\(a_1 = a, b_1 = 2 c_1 = – 9\)

\(a_2 = 3, b_2 = b c_2 = – 18\)

\(\frac{a_1}{a_2}\ = \frac{b_1}{b_2}\)

\(\frac{a}{3}\ = \frac{2}{b}\)

ab =6

Ans:- option (d)

Ans:- Option (b)

Solution:- Option (a)

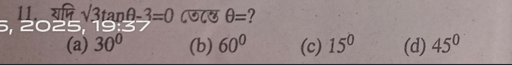
Solution:- Option (b)

= \( \sqrt3\)× tan 60 – 3

= \( \sqrt3\) ×\( \sqrt3\) – 3 = 3 – 3 = 0

Solution:- Option (A)

কোনো এডাল লেখৰ শূণ্য হবলৈ হলে সেই বিন্দুটোৰ মাজেৰে লেখডাল যাব লাগিব

Solution:-

Given , \(a_n = 7n – 4\)

\(a_1 = 3)

\(a_2 = 10)

\(a_3 = 17)

d = 10 – 3 = 7

Ans:- Option (a)

Ans:- Option (b)

Solution:-

we know that,

sin 30 = 1/2

cos 60 = 1/2

A + B = 30 + 60 = 90

Ans:- Option (b)

Solution:-

we know that

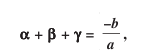
So, Option (d)

Solution:-

A/q

2πrh = 264

πrh = 132

π\(r^2\)h = 924

132r = 924

r = 7

So, 2πrh = 264

= 2 × \(\frac{22}{7}\)×7 × h =264

= 44h = 264

= h = 6

ব্যাস = 14

ব্যাস : উচ্চতা

14 : 6

7 : 3

Ans:- Option (b)

Solution:- ধৰো, ব্যাসাৰ্ধ = r

চুঙাটোৰ উচ্চতা = 5

চুঙাৰ আয়তন = শংকুৰ আয়তন

π\(r^2\)h = 1/3 π\(r^2\)h

5 = 1/3 h

h = 15

So, Option (b)