বৃত্ত সম্বন্ধীয় কালি Class 10 Maths Solution in Assamese medium Chapter 12 Exercise 12.1 Solution Seba Board Assam অনুশীলনী 12.2
অনুশীলনী 12.2
(অন্যধৰণে দিয়া নাথাকিলে π = 22/7 ল’বা)
1. 6 চে.মি. ব্যাসার্দ্ধযুক্ত এটা বৃত্তৰ এটা বৃত্তকলাৰ কালি নির্ণয় কৰা, যদি বৃত্তকলাটোৰ কোণ 60° হয়।
\(Solution:-\)
প্ৰশ্নমতে, বৃত্তকলাটোৰ কোণ \(= 60^\circ\)।
আমি জানো, বৃত্তকলাৰ ক্ষেত্ৰফল \(= \frac{\theta}{360^\circ} \times \pi r^2\)।
\(\therefore 60^\circ \) কোণযুক্ত বৃত্তকলাৰ ক্ষেত্ৰফল \(\frac{60^\circ}{360^\circ} \times \pi r^2\) ছেমি\(^{2}\)
\(=\frac{36}{6} \pi\) ছেমি\(^{2}\)
\(= 6\times \frac{22}{7}\) ছেমি\(^{2}\)
\(=\frac{132}{7}\) ছেমি\(^{2}\)
2. 22 চে.মি. পৰিধিযুক্ত এটা বৃত্তৰ এটা চোকৰ কালি নির্ণয় কৰা।
\(Solution:- \) বৃত্তৰ পৰিধি C = 22 ছেমি (দিয়া আছে)
উল্লেখযোগ্য যে, বৃত্তৰ এটা কোয়াড্ৰেণ্ট হৈছে এটা বৃত্তকলা যিয়ে \(90^\circ \) কোণ সৃষ্টি কৰে।
ধৰা হ’ল বৃত্তৰ ব্যাসাৰ্দ্ধ \(= r\)
যিহেতু, \(C = 2 \pi r = 22,\)
\(r = \frac{22}{2 \pi} = \frac{7}{2} \) ছেমি।
\(\therefore \frac{\theta}{360^\circ} \times \pi r^2।\)
এতিয়া, \(\theta = 90^\circ\)
\(\ A = \frac{90^\circ}{360^\circ} \times \pi r^2 \)
\(A = \frac{49}{16} \pi \)
\(A= \frac{77}{8} \) = 9.6 ছেমি\(^{2}\)
3. এটা ঘড়ীৰ মিনিটৰ কাঁটাডালৰ দৈর্ঘ্য 14 চে.মি.। 5 মিনিটত ঘড়ীৰ কাঁটাডালৰ দ্বাৰা ঘূৰণৰ কালি নির্ণয় কৰা।
Solution:-
মিনিট সূঁচৰ দৈৰ্ঘ্য = ঘড়ীৰ ব্যাসাৰ্দ্ধ (বৃত্ত)
বৃত্তৰ ব্যাসাৰ্দ্ধ (r) = 14 ছেমি (দিয়া আছে)
60 মিনিটত সূঁচটোৱে সৃষ্টি কৰা কোণ \(= 360^\circ\)
5 মিনিটত সূঁচটোৱে সৃষ্টি কৰা কোণ \(= 360^\circ \times \frac{5}{60} = 30^\circ\)
আমি জানা যে ,
বৃত্তকলাৰ ক্ষেত্ৰফল = \(\frac{\theta}{360^\circ} \times \pi r^2\)
এতিয়া, \(30^\circ\) কোণ সৃষ্টি কৰা বৃত্তকলাৰ ক্ষেত্ৰফল \( = \frac{30^\circ}{360^\circ} \times \pi r^2 \) ছেমি\(^{2}\)
\(=\frac{1}{12} \times \pi \times 14^2\)
\(=\frac{49}{3} \times \frac{22}{7} \) ছেমি\(^{2}\)
\(=\frac{154}{3} \approx 51.33 \) ছেমি\(^{2}\)
4. 10 চে.মি. ব্যাসার্দ্ধৰ এটা বৃত্তৰ এডাল জ্যাই কেন্দ্ৰত এটা সমকোণ কৰে। অনুৰূপ
(i) গৌণ বৃত্তখণ্ড
(ii) মুখ্য বৃত্তকলাৰ কালি নিৰ্ণয় কৰা। (ব্যৱহাৰ কৰা π = 3.14)
Solution:-
এতিয়া, AB হ’ল এটা জ্যামিতি যি কেন্দ্ৰ O-ত \(90^\circ\) কোণ সৃষ্টি কৰিছে।
দিয়া আছে, বৃত্তৰ ব্যাসাৰ্দ্ধ \(r = 10\) ছেমি।
(i) গৌণ বৃত্তকলাৰ ক্ষেত্ৰফল \( \frac{90}{360^\circ} \times \pi r^2 \)
\(= \frac{1}{4} \times \frac{22}{7} \times 10^2\)
∴ গৌণ বৃত্তকলাৰ ক্ষেত্ৰফল \( 78.5 \) ছেমি²।
পুনৰ, \( \triangle AOB \) ৰ ক্ষেত্ৰফল \( \frac{1}{2} \times OB \times OA \)
এতিয়া, OB আৰু OA বৃত্তৰ ব্যাসাৰ্দ্ধ, অৰ্থাৎ \( 10 \) ছেমি।
\(\triangle AOB = \frac{1}{2} \times 10 \times 10\)
\(= 50 \) ছেমি²।
এতিয়া, গৌণ খণ্ডৰ ক্ষেত্ৰফল = গৌণ বৃত্তকলাৰ ক্ষেত্ৰফল – \(\triangle AOB \)
\(= 78.5 – 50\)
\(= 28.5 \) ছেমি²
(ii) মুখ্য বৃত্তকলাৰ ক্ষেত্ৰফল = বৃত্তৰ ক্ষেত্ৰফল – গৌণ বৃত্তকলাৰ ক্ষেত্ৰফল
\(= (3.14 \times 10^2) – 78.5\)
\(= 314 – 78.5 = 235.5 \) ছেমি²।
5. 21 চে.মি., ব্যাসার্দ্ধৰ এটা বৃত্তত, এটা চাপে কেন্দ্রত এটা 60° ৰ কোণ কৰে। নির্ণয় কৰাঃ
(i) চাপটোৰ দৈর্ঘ্য।
(ii) চাপটোৰ দ্বাৰা গঠন হোৱা বৃত্তকলাটোৰ কালি।
(iii) অনুৰূপ জ্যাডালৰ দ্বাৰা গঠন হোবা বৃত্তখণ্ডটোৰ কালি।
Solution:_
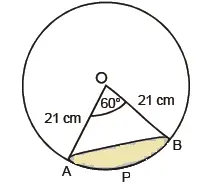
Solutionm:-
দিয়া আছে,
বৃত্তৰ ব্যাসাৰ্দ্ধ \(r = 21\) ছেমি।
\(\theta = 60^\circ\)
(i) জ্যা AB ৰ দৈৰ্ঘ্য \(\frac{\theta}{360^\circ} \times \)বৃত্তৰ পৰিধি \(2\pi r\)
∴ জ্যা AB ৰ দৈৰ্ঘ্য = \(\frac{60^\circ}{360^\circ} \times 2 \times \frac{22}{7} \times 21\)
\(\ = \frac{1}{6} \times 2 \times \frac{22}{7} \times 21\)
অথবা, জ্যা AB ৰ দৈৰ্ঘ্য = 22 ছেমি
(ii) জ্যা AB ৰ সৃষ্টি কৰা কোণ \(60^\circ\)
\(\text{∴ } 60^\circ \) কোণ সৃষ্টি কৰা ক্ষেত্ৰফল =\(\frac{60^\circ}{360^\circ} \times \pi r^2 \) ছেমি²
\(\ = \frac{441}{6} \times \frac{22}{7} \)ছেমি²
∴ বৃত্তকলাৰ ক্ষেত্ৰফল } = 231 ছেমি²।
(iii) ক্ষেত্ৰফল APB খণ্ড = \(\text{ক্ষেত্ৰফল OAPB – }\triangle OAB\)
যিহেতু, \(\triangle OAB\) ৰ বাহুদ্বয় বৃত্তৰ ব্যাসাৰ্দ্ধ, আৰু সৃষ্টি কৰা কোণ \(60^\circ\),
সেয়ে \(\triangle OAB\) এটা সমবাহু ত্ৰিভুজ।
\(\text{∴ } \triangle OAB \) ৰ ক্ষেত্ৰফল = \(\frac{\sqrt{3}}{4} \times a^2 \) ছেমি\(^{2}\)
APB খণ্ডৰ ক্ষেত্ৰফল \(= 231 – \frac{\sqrt{3}}{4} \times 21^2\)
\(\ = 231 – \frac{441 \sqrt{3}}{4} \) ছেমি\(^{2}\)
∴ APB খণ্ডৰ ক্ষেত্ৰফল = \(\left[ 231 – \frac{441 \sqrt{3}}{4} \right]\) ছেমি\(^{2}\)
6. 15 চে.মি. ব্যাসার্দ্ধৰ এটা বৃত্তৰ এডাল জ্যাই কেন্দ্ৰত এটা 60° ৰ কোণ কৰে। বৃত্তটোৰ অনুৰূপ গৌণ আৰু মুখ্য বৃত্তখণ্ডবোৰৰ কালি নির্ণয় কৰা।
\(Solution:-\)
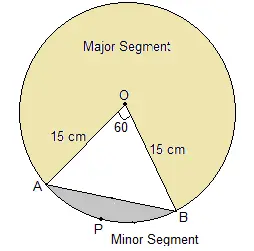
দিয়া আছে,
বৃত্তৰ ব্যাসাৰ্দ্ধ \(r = 15\) ছেমি।
\(\theta = 60^\circ\)
∴ ক্ষেত্ৰফল OAPB \( = \frac{60^\circ}{360^\circ} \times \pi r^2 \) ছেমি\(^{2}\)
\(\ = \frac{225}{6} \pi \) ছেমি\(^{2}\)
\(\triangle AOB\) এটা সমবাহু ত্ৰিভুজ, যিহেতু বাহুদ্বয় বৃত্তৰ ব্যাসাৰ্দ্ধ আৰু সৃষ্টি কৰা কোণ \(60^\circ\)।
\(\text{∴ }\triangle AOB \) ৰ ক্ষেত্ৰফল = \(\frac{\sqrt{3}}{4} \times a^2 \)ছেমি\(^{2}\)
\(\ = \frac{\sqrt{3}}{4} \times 15^2 \) ছেমি\(^{2}\)
\(\text{∴ }\triangle AOB \) ৰ ক্ষেত্ৰফল \(= 97.31 \) ছেমি\(^{2}\)
APB খণ্ডৰ ক্ষেএত্রফল = OAPB ক্ষেত্ৰফল – \(\triangle AOB\)
অথবা, APB খণ্ডৰ ক্ষেত্ৰফল = \(\left( \frac{225}{6} \pi – 97.31 \right)\) ছেমি\(^{2}\)
∴ APB খণ্ডৰ ক্ষেত্ৰফল \(= 20.43 \) ছেমি\(^{2}\)
এতিয়া, বৃহৎ খণ্ডৰ ক্ষেত্ৰফল = বৃত্তৰ ক্ষেত্ৰফল – APB খণ্ডৰ ক্ষেত্ৰফল
অথবা, বৃহৎ খণ্ডৰ ক্ষেত্ৰফল \(= \pi \times 15^2 – 20.4 \) ছেমি\(^{2}\)
∴ বৃহৎ খণ্ডৰ ক্ষেত্ৰফল = 686.06 ছেমি\(^{2}\)
7. 12 চে.মি. ব্যাসাৰ্দ্ধৰ এটা বৃত্তৰ এডাল জ্যাই কেন্দ্রত এটা 120° ৰ কোণ কৰে। বৃত্তটোৰ অনুৰূপ বৃত্তখণ্ডটোৰ কালি নিৰ্ণয় কৰা। (ব্যৱহাৰ কৰা = 3.14 আৰু √3= 1.73)
\(Solution:-\)
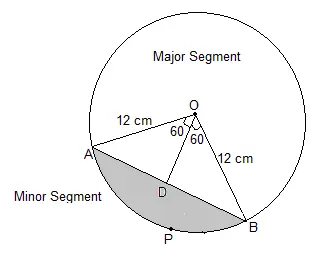
Solution:-
দিয়া আছে,
বৃত্তৰ ব্যাসাৰ্দ্ধ \(r = 12\) ছেমি।
এতিয়া, AB জ্যাৰ ওপৰত OD লম্ব আঁকা হ’ল, যিয়ে জ্যাটোক দ্বিখণ্ডিত কৰে।
∴ AD = DB
ক্ষুদ্র খণ্ডৰ ক্ষেত্ৰফল = \(\frac{\theta}{360^\circ} \times \pi r^2\)
∴ \(\frac{120}{360} \times \frac{22}{7} \times 12^2\) ছেমি²।
∴ ক্ষেত্ৰফল \(150.72\) ছেমি²।
\(\triangle AOB\) লৈ বিবেচনা কৰা হ’ল,
\(\implies\angle OAB = 180^\circ – (90^\circ + 60^\circ) = 30^\circ\)
এতিয়া, \(\implies\cos 30^\circ = \frac{AD}{OA}\)
\(\implies\frac{\sqrt{3}}{2} = \frac{AD}{12}\)
অথবা, AD \(= 6 \sqrt{3}\) ছেমি।
OD, AB জ্যাৰ দ্বিখণ্ডক। সেয়ে,
AB \(= 2 \times AD = 12 \sqrt{3}\) ছেমি।
এতিয়া, \(\sin 30^\circ = \frac{OD}{OA}\)
\(\frac{1}{2} = \frac{OD}{12}\)
∴ OD \(= 6\) ছেমি।
∴ \(\triangle AOB\) ৰ ক্ষেত্ৰফল \(= \frac{1}{2} \times \text{base} \times \text{height}\)
এতিয়া, base \(\implies = AB = 12 \sqrt{3}\) আৰু height \(= 6\)
∴ \(\triangle AOB\) ৰ ক্ষেত্ৰফল \(= \frac{1}{2} \times 12 \sqrt{3} \times 6\) ছেমি²।
∴ \(\triangle AOB\) ৰ ক্ষেত্ৰফল \(= 36 \sqrt{3}\) ছেমি²।
অথবা, \(\triangle AOB\) ৰ ক্ষেত্ৰফল \(= 62.28\) ছেমি²।
সংশ্লিষ্ট ক্ষুদ্র খণ্ডৰ ক্ষেত্ৰফল = ক্ষুদ্র খণ্ডৰ ক্ষেত্ৰফল – \(\triangle AOB\)
∴ ক্ষেত্ৰফল \(= 150.72 – 62.28\) ছেমি²।
∴ সংশ্লিষ্ট ক্ষুদ্র খণ্ডৰ ক্ষেত্ৰফল \(= 88.44\) ছেমি²।
8. 15 মিটাৰ বাহুৰ এখন বৰ্গক্ষেত্ৰাকাৰ ঘাঁহনি পথাৰৰ এটা চুকত এটা খুঁটিত 5 মিটাৰ দীঘল ৰছীৰে এটা ঘোঁৰা বান্ধি থোৱা হৈছে। (চিত্র 12.11)
(i) ঘোঁৰাটো য’ত চৰিব পাৰে পথাৰ খনৰ সেই অংশটোৰ কালি নিৰ্ণয় কৰা।
(ii) যদি ৰছীডাল 5 মিটাৰৰ সলনি 10 মিটাৰ দীঘল হয়, চৰণীয়া অঞ্চলটোৰ বৃদ্ধি নিৰ্ণয় কৰা। (ব্যৱহাৰ কৰা π = 3.14)

\(Solution:-\)
ঘোঁড়াটো যদি চতুষ্কোণ ক্ষেত্ৰখনৰ এটা মূৰত বান্ধি থোৱা হয়, তেন্তে সেইটো কেৱল ক্ষেত্ৰখনৰ \(\frac{1}{4}\) অংশ (অর্থাৎ, \(90^\circ\) কোণ থকা ক্ষেত্ৰফল) চৰুৱাব পাৰে।
ইয়াত, দড়িখনৰ দৈৰ্ঘ্য হ’ব বৃত্তৰ অৰ্ধব্যাস, অৰ্থাৎ \(r = 5 \), মিটাৰ\(^{2}\)
ক্ষেত্ৰখনৰ একোণ দৈৰ্ঘ্য \(= 15 \), মিটাৰ\(^{2}\)
(i) বৃত্তৰ ক্ষেত্ৰফল:
বৃত্তৰ ক্ষেত্ৰফল\( = \pi r^2 = \frac{22}{7} \times 5^2 = 78.5 \), মিটাৰ\(^{2}\)
এতিয়া, ঘোঁড়াই চৰুৱাব পৰা অংশৰ ক্ষেত্ৰফল:
ঘোঁড়াই চৰুৱাব পৰা অংশ = \(\frac{1}{4} \times 78.5 = \frac{78.5}{4} = 19.625 \), মিটাৰ\(^{2}\)
(ii) যদি দড়িখনৰ দৈৰ্ঘ্য ১০ মিটাৰ কৰা হয়, তেন্তে:
বৃত্তৰ ক্ষেত্ৰফল = \(\pi r^2 = \frac{22}{7} \times 10^2 = 314 \), মিটাৰ\(^{2}\)
এতিয়া, ঘোঁড়াই চৰুৱাব পৰা অংশ:
ঘোঁড়াই চৰুৱাব পৰা অংশ \(= \frac{1}{4} \times 314 = \frac{314}{4} = 78.5 \), মিটাৰ\(^{2}\)
∴ চৰুৱাব পৰা ক্ষেত্ৰফল বৃদ্ধি:
বৃদ্ধি \(= 78.5 – 19.625 = 58.875 \), মিটাৰ\(^{2}\)
9. 35 মি.মি. ব্যাসযুক্ত এটা বৃত্তৰ আকাৰৰ এটা ব্ৰোচপিন ৰূপৰ তাঁৰেৰে তৈয়াৰ কৰা হৈছে। আকৌ, তাঁৰডাল 5 ডাল ব্যাস হোৱাকৈ ব্যৱহাৰ কৰা হৈছে আৰু চিত্ৰ 12.12ত দেখুওৱাৰ দৰে এই ব্যাসবোৰে বৃত্তটোক 10 টা সমান বৃত্তকলাত ভাগ কৰিছে।
(i) প্রয়োজন হোৱা ৰূপৰ তাঁৰৰ মুঠ দৈর্ঘ্য নিৰ্ণয় কৰা।
(ii) ব্ৰোচপিনটোৰ প্ৰতিটো বৃত্তকলাৰ কালি নিৰ্ণয় কৰা।

Solution:-
ব্যাস \(D = 35\) মিমি
মুঠ ব্যাসৰ সংখ্যা যিবোৰ বিবেচনা কৰিব লাগিব = 5
এতিয়া, 5 টা ব্যাসৰ মুঠ দৈৰ্ঘ্য লাগিব:
\(35 \times 5 = 175\) মিমি
বৃত্তৰ পৰিধি: \(C = 2 \pi r\) বা, \(C = \pi D = \frac{22}{7} \times 35 = 110\) মিমি
বৃত্তৰ ক্ষেত্ৰফল: \(A = \pi r^2\) বা, \(A = \frac{22}{7} \times \left(\frac{35}{2}\right)^2 = \frac{1925}{2}\) মিমি\(^2\)
(i) মুঠ ৰূপৰ তাঁৰৰ দৈৰ্ঘ্য লাগিব:
বৃত্তটোৰ পৰিধি + 5 ডাল ব্যাসৰ দৈৰ্ঘ্য \(= 110 + 175 = 285\) মিমি
(ii) ব্ৰোচত মুঠ খণ্ডৰ সংখ্যা = 10
এতিয়া, প্ৰতিখন খণ্ডৰ ক্ষেত্ৰফল:
বৃত্তকলাটোৰ কালি \(= \frac{\text{Total area of the circle}}{\text{Number of sectors}}\)
\(\therefore\) বৃত্তকলাটোৰ কালি \(= \frac{1925}{2} \times \frac{1}{10} = \frac{385}{4}\) মিমি\(^2\)
10. এটা ছাতিৰ সমান ব্যৱধানত থকাকৈ 8 ডাল ৰিব্ আছে (চিত্র 12.13 চোৱা)। ছাতিটোক 45 চে.মি. ব্যাসার্দ্ধৰ এটা সমান বৃত্ত হ’ব বুলি ধৰি লৈ, ছাতিটোৰ দুটা ক্রমিক ৰিবৰ মাজৰ কালি নিৰ্ণয় কৰা।
\(Solution:-\)
ছাতিটো ঠিয়া নথকা অৱস্থাত ব্যাসাৰ্ধ \(r = 45\) ছেমি
তেন্তে, বৃত্তটোৰ ক্ষেত্ৰফল \(A = \pi r^2 = \frac{22}{7} \times (45)^2 = 6364.29\) ছেমি\(^2\)
মুঠ পাত (\(n\)) = 8
\(\therefore\) ছাতিটোৰ দুটা ক্ৰমাগত পাতৰ মাজৰ ক্ষেত্ৰফল \(= \frac{A}{n}\)
\(\frac{6364.29}{8}\) ছেমি\(^2\)
বা, ছাতিটোৰ দুটা ক্ৰমাগত পাতৰ মাজৰ ক্ষেত্ৰফল \(= 795.5\) ছেমি\(^2\)
11. এখন গাড়ীৰ ওপৰাউপৰিকৈ লাগি নথকাকৈ দুডাল ৱাইপাৰ (Wiper) আছে। 115° ৰ এটা কোণৰে ঘূৰি থকা প্রতিডাল ৱাইপাৰৰ 25 চে.মি. দৈৰ্ঘ্যৰ এখন ব্লেড আছে। ব্লেডবোৰৰ প্রতিটো ঘূৰণত পৰিষ্কাৰ হোৱা মুঠ অংশৰ কালি নির্ণয় কৰা।
\(Solution:-\)
দিয়া আছে,
ব্যাসাৰ্ধ \(r = 25\) ছেমি
খণ্ড কোণ \(\theta = 115^\circ\)
যিহেতু 2 টা ব্লেড আছে,
তেন্তে, ৱাইপাৰটোৱে সৃষ্টি কৰা খণ্ডটোৰ মুঠ ক্ষেত্ৰফল \(= 2 \times \frac{\theta}{360^\circ} \times \pi r^2\)
\(= 2 \times \frac{115}{360} \times \frac{22}{7} \times 25^2\)
\(= 2 \times \frac{158125}{252} \), ছেমি\(^2\)
\(= \frac{158125}{126} = 1254.96 \), ছেমি\(^2\)
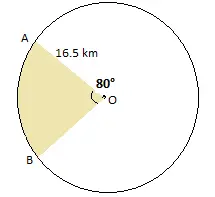
12. পানীৰ তলত থকা শিলবোৰৰ বাবে জাহাজবোৰক সতৰ্ক কৰি দিবলৈ, এটা লাইটহাউচে ৰঙা বৰণীয়া পোহৰ 16.5 কি.মি. দূৰত্বলৈ 80° কোণৰ এটা বৃত্তকলাৰ ওপৰত বিয়পায়। সাগৰৰ যি অঞ্চলৰ ওপৰত জাহাজবোৰ সতর্ক কৰি দিয়া হয় সেই অংশৰ কালি নির্ণয় কৰা। (ব্যৱহাৰ কৰা π = 3.14)।
Solution:-
লাইটহাউচটোৰ অৱস্থান \(O\) বুলি ধৰোঁ।
ইয়াত, ব্যাসাৰ্ধ হ’ব সেই দূৰত্ব যিমান দূৰলৈ আলো বিস্তাৰিত হয়।
দিয়া আছে, ব্যাসাৰ্ধ \(r = 16.5\) কিমি
খণ্ড কোণ \(\theta = 80^\circ\)
এতিয়া, যিমান সমুদ্ৰাঞ্চলত জাহাজসমূহ সতৰ্ক কৰা হয় তাৰ মুঠ ক্ষেত্ৰফল = খণ্ডটোৱে সৃষ্টি কৰা ক্ষেত্ৰফল
বা, খণ্ডটোৰ ক্ষেত্ৰফল:
\(\text{Area of sector} = \frac{\theta}{360^\circ} \times \pi r^2\)
\(=\frac{80^\circ}{360^\circ} \times \pi \times (16.5)^2 \), কিমি\(^2\)
\(= 189.97 \), কিমি\(^2\)
13. চিত্র 12.14 ত দেখুওৱাৰ দৰে এখন ঘূৰণীয়া টেবুল কভাৰৰ ছয়টা সমান নক্সা আছে। যদি কভাৰটোৰ ব্যাসার্দ্ধ 28 চে.মি. হয়, তেন্তে প্রতি চে.মি.² ত 0.35 টকা হাৰত নক্সাবোৰ তৈয়াৰ কৰাৰ খৰচ নিৰ্ণয় কৰা। (ব্যৱহাৰ কৰা √3 = 1.7)
Solution:-
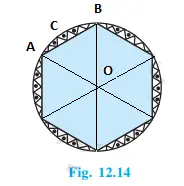
মুঠ সমান নক্সাৰ সংখ্যা = 6
\(\angle AOB = \frac{360^\circ}{6} = 60^\circ\)
কভাৰৰ ব্যাসাৰ্ধ = 28 ছেমি
নক্সা তৈয়াৰৰ ব্যয় = ₹ 0.35 প্ৰতি ছেমি\(^2\)
যিহেতু ত্ৰিভুজটোৰ দুই বাহু বৃত্তটোৰ ব্যাসাৰ্ধ আৰু কোণ 60° হয়, সেয়ে \(\triangle AOB\) হ’ল সমবাহু ত্ৰিভুজ।
তেন্তে, তাৰ ক্ষেত্ৰফল = \(\frac{\sqrt{3}}{4} \times a^2\)
ইয়াত, \(a = OA\)
\(\therefore\) সমবাহু \(\triangle AOB\) ৰ ক্ষেত্ৰফল = \(\frac{\sqrt{3}}{4} \times 28^2 = 333.2\) ছেমি\(^2\)
খণ্ড \(ACB\) ৰ ক্ষেত্ৰফল = \(\frac{60^\circ}{360^\circ} \times \pi r^2\)
\(= 410.66\) ছেমি\(^2\)
এতিয়া, এখন নক্সাৰ ক্ষেত্ৰফল = খণ্ড \(ACB\) ৰ ক্ষেত্ৰফল – \(\triangle AOB\) ৰ ক্ষেত্ৰফল
\(= 410.66 – 333.2 = 77.46 \), ছেমি \(^2\)
\(\therefore\) 6 টা নক্সাৰ মুঠ ক্ষেত্ৰফল = \(6 \times 77.46 = 464.76\) ছেমি\(^2\)
সেয়ে, নক্সা তৈয়াৰৰ মুঠ ব্যয় = \(464.76 \times 0.35 = ₹ 162.66\)
R ব্যাসার্দ্ধ যুক্ত এটা বৃত্তৰ p (ডিগ্ৰীত) কোণৰ এটা বৃত্তকলাৰ কালি হ’ল–
\(\text{(A)} \left(\frac{p}{180} \times 2\pi R \right)\)
\(\text{(B)} \left(\frac{p}{180} \times \pi R^2 \right)\)
\(\text{(C)} \left(\frac{p}{360} \times 2\pi R \right)\)
\(\text{(D)} \left(\frac{p}{720} \times 2\pi R^2 \right)\)
উত্তৰঃ বৃত্তৰ খণ্ডৰ ক্ষেত্ৰফল = \(\left(\frac{\theta}{360^\circ}\right) \times \pi R^2\)
যিহেতু, \(\theta = p\)
সেয়ে, বৃত্তৰ খণ্ডৰ ক্ষেত্ৰফল = \(\frac{p}{360} \times \pi R^2\)
একেলগে 2 ৰে গুণ আৰু ভাগ কৰিলে,
\(= \left(\frac{p}{360}\right) \times \frac{2}{2} \times \pi R^2\)
\(= \left(\frac{2p}{720}\right) \times 2\pi R^2\)
শুদ্ধ উত্তৰটো (D)
