অনুশীলনী 12.3
বৃত্ত সম্বন্ধীয় কালি Class 10 Maths Solution in Assamese medium Chapter 12 Exercise 12.3 Solution Seba Board Assam অনুশীলনী 12.3
(অন্যধৰণে উল্লেখ নাথাকিলে, π = 22/7 ল’বা।)
1. চিত্র 12.19 ত, আচ্ছাদিত অঞ্চলটোৰ কালি উলিওৱা, যদি PQ = 24 চে.মি., PR = 7 চে.মি. আৰু বৃত্তটোৰ কেন্দ্র O।
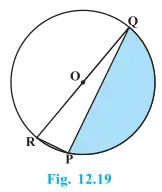
\(Solution:-\)
এয়া, P অর্ধ-বৃত্তত অৱস্থিত, সেয়ে,
\(P = 90^\circ\)
সেয়ে, QR বৃত্তৰ অতিভুজ আৰু ই বৃত্তৰ ব্যাসৰ সমান।
\(\therefore QR = D\)
পাইথাগোৰাচ সূত্র অনুযায়ী,
\(QR^2 = PR^2 + PQ^2\)
অথবা,
\(QR^2 = 7^2 + 24^2\)
\(QR = 25 \)
সেয়ে, বৃত্তৰ ব্যাসার্ধ = \(\frac{25}{2}\)
এতিয়া, অর্ধ-বৃত্তৰ ক্ষেত্ৰফল\(=\frac{\pi R^2}{2}\)
\(=\frac{22}{7} \times \frac{25}{2} \times \frac{25}{2} \div 2 \)
\(=\frac{13750}{56} cm^2 = 245.54 \)
পুনৰ, \( \triangle PQR \) ৰ ক্ষেত্ৰফল
\(=\frac{1}{2} \times PR \times PQ\)
\(=\left(\frac{1}{2}\right) \times 7 \times 24 \)
\(= 84 cm^2\)
সেয়ে, ৰং কৰা অংশৰ ক্ষেত্ৰফল
\(= 245.54 – 84 \)
\(= 161.54 \) \(cm^2\)
2. চিত্র 12.20ত, আচ্ছাদিত অঞ্চলটোৰ কালি নিৰ্ণয় কৰা যদি O কেন্দ্র যুক্ত ঐককেন্দ্রিক বৃত্ত দুটাৰ ব্যাসার্দ্ধ ক্রমে 7 চে.মি. আৰু 14 চে.মি. আৰু ∠AOC = 40°.
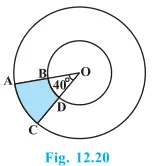
Solution:-
দিয়াঁ হয়,
সেক্টৰৰ সৃষ্টি কৰা কোণ = \(40^\circ\),
অভ্যন্তৰীণ বৃত্তৰ ব্যাসাৰ্ধ = \(r = 7 cm,\) আৰু
বাহ্যিক বৃত্তৰ ব্যাসাৰ্ধ = \(R = 14 cm\)
আমাৰ জনা আছে,
সেক্টৰৰ ক্ষেত্ৰফল = \(\left(\frac{\theta}{360^\circ}\right) \times \pi r^2\)
সেয়ে, OAC ৰ ক্ষেত্ৰফল
\(\left(\frac{40^\circ}{360^\circ}\right) \times \pi R^2 \ cm^2\)
= \(68.44 cm^2\)
OBD ৰ ক্ষেত্ৰফল
\(\left(\frac{40^\circ}{360^\circ}\right) \times \pi r^2 \ cm^2\)
\(\left(\frac{1}{9}\right) \times \frac{22}{7} \times 7^2 = 17.11 \ cm^2\)
এতিয়া, ABDC ৰ ৰং কৰাৰ অংশৰ ক্ষেত্ৰফল
OAC ৰ ক্ষেত্ৰফল – OBD ৰ ক্ষেত্ৰফল
= \(68.44 – 17.11 \)
= \(51.33 \;\; \ cm^2\)
3. চিত্র 12.21 ত. আচ্ছাদিত অঞ্চলটোৰ কালি নির্ণয় কৰা, যদি 14 চে.মি. বাহুৰ ABCD এটা বর্গক্ষেত্র আৰু APD আৰু BPC অর্ধবৃত্ত হয়।
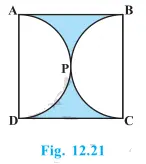
Solution:-
ABCD বৰ্গৰ পাৰ্শ্ব (দিয়াঁ হৈছে) = 14 cm
সেয়ে, ABCD ৰ ক্ষেত্ৰফল = \(a^2\)
= \(14 \times 14 cm^2 = 196 \ cm^2\)
আমাৰ জনা আছে যে, বৰ্গৰ পাৰ্শ্ব = বৃত্তৰ ব্যাস = 14 cm
সেয়ে, বৰ্গৰ পাৰ্শ্ব = অর্ধ-বৃত্তৰ ব্যাস = 14 cm
\(\therefore\) অর্ধ-বৃত্তৰ ব্যাসাৰ্ধ = 7 cm
এতিয়া, অর্ধ-বৃত্তৰ ক্ষেত্ৰফল
\(=\frac{\pi R^2}{2}\)
= \(\frac{\frac{22}{7} \times 7 \times 7}{2} \ cm^2\)
= \(77 cm^2\)
\(\therefore\) দুটা অর্ধ-বৃত্তৰ ক্ষেত্ৰফল
\(2 \times 77 cm^2 = 154 cm^2\)
সেয়ে, শ্বেডেড অংশৰ ক্ষেত্ৰফল
= বৰ্গৰ ক্ষেত্ৰফল – দুটা অর্ধ-বৃত্তৰ ক্ষেত্ৰফল
= \(196 – 154 \)
= \(42 cm^2\)
4. চিত্র 12.22ত আচ্ছাদিত অঞ্চলটোৰ কালি নির্ণয় কৰা য’ত 12 চে.মি. বাহুৰ এটা সমবাহু ত্রিভুজৰ শীর্ষ বিন্দু Oক কেন্দ্র হিচাবে ধৰি 6 চে.মি. ব্যাসার্দ্ধ এটা বৃত্তীয় চাপ আঁকা হৈছে।
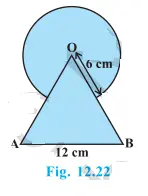
Solution:-
এনেধৰণে দিয়া আছে যে \(OAB\) এটা সমবাহু ত্ৰিভুজ য’ত প্ৰত্যেক কোণ \(60^\circ\)।
বৃত্ত আৰু ত্ৰিভুজৰ মাজত সাধাৰণ অঞ্চলটোৰ ক্ষেত্ৰফল সমান।
বৃত্তৰ ব্যাসাৰ্ধ: \(6 \, \text{cm}\)
ত্ৰিভুজৰ প্ৰান্তভাগ: \(12 \, \text{cm}\)
ত্ৰিভুজৰ ক্ষেত্ৰফল:
সমবাহু ত্ৰিভূজৰ কালি
= \(\frac{\sqrt{3}}{4} \times (OA)^2\)
= \(\frac{\sqrt{3}}{4} \times 12^2\) = \(36 \sqrt{3} \, \text{cm}^2)\)
বৃত্তৰ ক্ষেত্ৰফল:
\(\text{Area of the circle} = \left(\pi R^2\right) = \left(\frac{22}{7} \times 6^2\right) = \left(\frac{792}{7} \, \text{cm}^2\right)\)
বৃত্তৰ খণ্ডৰ ক্ষেত্ৰফল (৬০° কোণৰ বাবে)
\(\text{Area of the sector} = \left(\frac{60^\circ}{360^\circ} \times \pi r^2\right)\)
\(= \left(\frac{1}{6} \times \frac{22}{7} \times 6^2\right) \)
\(= \left(\frac{132}{7} \, \text{cm}^2\right)\)
ৰং কৰা অংশৰ কালি = ত্ৰিভূজৰ কালি + বৃত্তৰ কালি – বৃত্তকলাৰ কালি
\(=\left(36 \sqrt{3} + \frac{792}{7} – \frac{132}{7} \, \text{cm}^2\right)\)
\(=\left(36 \sqrt{3} + \frac{660}{7}\right) \, \text{cm}^2\)
5. চিত্র 12.23ত দেখুওৱাৰ দৰে 4 চে.মি. বাহুৰ এটা বৰ্গক্ষেত্ৰৰ প্ৰতিটো চুকৰপৰা 1 চে.মি. ব্যাসার্দ্ধৰ এটা বৃত্তৰ এটা চোক কাটি লোৱা হৈছে আৰু 2 চে.মি. ব্যাসৰ এটা বৃত্তও কাটি লোৱা হৈছে। বর্গক্ষেত্ৰটোৰ অৱশিষ্ট অংশৰ কালি নিৰ্ণয় কৰা।
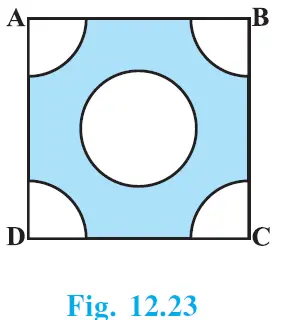
Solution:-
দিয়া আছে —
বৰ্গাকাৰৰ বাহু = \(4 cm\)
বৃত্তৰ ব্যাসাৰ্ধ = \(1 cm\)
বৰ্গাকাৰ ক্ষেত্ৰফল = \( = 4^2 = 16 cm^2\)
একোণৰ চতুৰ্থাংশ ক্ষেত্ৰফল = \(\frac{\pi R^2}{4} = \frac{22}{7} \times \frac{1^2}{4} = \frac{11}{14} \, \text{cm}^2\)
4 টা একোণৰ চতুৰ্থাংশৰ মুঠ ক্ষেত্ৰফল =\( 4 \times \frac{11}{14} = \frac{22}{7} \, \text{cm}^2\)
মাজৰ বৃত্তৰ ক্ষেত্ৰফল = \(\pi R^2 = \frac{22}{7} \times 1^2 = \frac{22}{7} \, \text{cm}^2\)
ৰং কৰা অঞ্চলৰ ক্ষেত্ৰফল =বৰ্গৰ ক্ষেত্ৰফল – চাৰিটা কোণৰ কালি + বৃত্তৰ কালি
\(= 16 – \frac{22}{7} – \frac{22}{7} = \frac{68}{7} \, \text{cm}^2\)
6. চিত্র 12.24ত দেখুওৱাৰ দৰে 32 চে.মি. ব্যাসার্দ্ধৰ এখন বৃত্তীয় টেবুলকভাৰৰ মাজত ABC এটা সমবাহু ত্রিভুজ এৰি এটা নক্সা তৈয়াৰ কৰা হৈছে। নক্সাটোৰ কালি নির্ণয় কৰা।

Solution:-
বৃত্তৰ ব্যাসাৰ্ধ = \(32\) ছেমি
ত্ৰিভুজৰ মধ্যমা \(AD\) যি বৃত্তৰ কেন্দ্ৰৰ মাজেৰে গৈছে।
\(\implies BD = \frac{AB}{2}\)
যিহেতু \(AD\) হৈছে ত্ৰিভুজৰ মধ্যমা,
\(\therefore AO\) = বৃত্তৰ ব্যাসাৰ্ধ} = \(\frac{2}{3} AD\)
\(\implies \frac{2}{3} AD = 32\) ছেমি
\(\implies AD = 48\) ছেমি
ত্ৰিভুজ \(\triangle ADB\)-ত,
পিথাগোৰাছৰ সূত্ৰ অনুসৰি,
\(AB^2 = AD^2 + BD^2\)
\(\implies AB^2 = 48^2 + \left(\frac{AB}{2}\right)^2\)
\(\implies AB^2 = 2304 + \frac{AB^2}{4}\)
\(\implies \frac{3}{4} AB^2 = 2304\)
\(\implies AB^2 = 3072\)
\(\implies AB = 32 \sqrt{3}\) ছেমি
ত্ৰিভুজ \(\triangle ADB\)-ৰ ক্ষেত্ৰফল
\(= \frac{\sqrt{3}}{4} \times (32 \sqrt{3})^2 \) ছেমি \(^2\) =\( 768 \sqrt{3}\) ছেমি \(^2\)
বৃত্তৰ ক্ষেত্ৰফল \(= \pi R^2 = \frac{22}{7} \times 32 \times 32 = \frac{22528}{7}\) ছেমি \(^2\)
আকৃতিৰ ক্ষেত্ৰফল
\(= \frac{22528}{7} – 768 \sqrt{3}\) ছেমি\(^2\)
7. চিত্র 12.25 ত, 14 চে.মি. বাহুৰ ABCD এটা বর্গক্ষেত্র। A, B, C আৰু D কেন্দ্ৰযুক্ত চাৰিটা বৃত্ত আঁকা হ’ল, যাতে প্রতিটো বৃত্তই বাকী থকা তিনিটা বৃত্তৰ দুটাক বহিঃভাৱে স্পর্শ কৰে। আচ্ছাদিত অঞ্চলটোৰ কালি নির্ণয় কৰা।
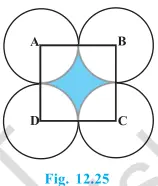
Solution:-
বৰ্গক্ষেত্ৰৰ পাৰ্শ্ব = \(14\) ছেমি
বৰ্গক্ষেত্ৰৰ চাৰিওফালে চাৰিখন চতুৰ্ভুজ অন্তৰ্ভুক্ত।
\(\therefore\) বৃত্তৰ ব্যাসাৰ্ধ = \(\frac{14}{2}\) ছেমি = \(7\) ছেমি
বৰ্গক্ষেত্ৰ \(ABCD\)-ৰ ক্ষেত্ৰফল
\(= 14^2 = 196 \) ছেমি\(^2\)
চতুৰ্ভুজৰ ক্ষেত্ৰফল
\(=\frac{\pi R^2}{4} = \frac{22}{7} \times 7^2 \div 4 \) ছেমি\(^2\)
\(= \frac{77}{2} \) ছেমি\(^2\)
চাৰিখন চতুৰ্ভুজৰ মুঠ ক্ষেত্ৰফল
\(=4 \times \frac{77}{2} = 154 \) ছেমি\(^2\)
আঁৰ লাগি থকা অংশৰ ক্ষেত্ৰফল
\( = 196 – 154 = 42 \) ছেমি\(^2\)
8. চিত্র 12.26 ত, এটা দৌৰা বাট দিয়া আছে, যাৰ বাওঁফাল আৰু সোঁফাল অর্ধবৃত্ত। ভিতৰৰ সমান্তৰাল ৰেখাখণ্ড দুটাৰ মাজত দূৰত্ব 60 মিটাৰ আৰু সেইবোৰ প্রত্যেকে 106 মিটাৰ দীঘল। যদি বাটটোৰ প্ৰস্থ 10 মিটাৰ হয়, তেন্তে নিৰ্ণয় কৰা:
(i) বাটটোৰ চাৰিওফালে ইয়াৰ ভিতৰৰ ফালৰ দূৰত্ব।
(ii) বাটটোৰ কালি।
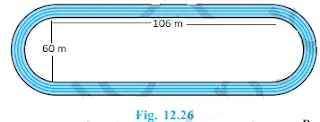
Solution:-
পথটোৰ প্ৰস্থ= 10 মি
দুটা সমান্তৰাল রেখাৰ মাজৰ দূৰত্ব = 60 মি
সমান্তৰাল পথটোৰ দৈৰ্ঘ্য = 106 মি
\( = DE = CF = 60 \) মি
ভিতৰৰ অর্ধবৃত্তৰ ব্যাসাৰ্ধ, \( r = OD = O’C\)
\(=\frac{60}{2} \) মি = 30 মি
বাহিৰৰ অর্ধবৃত্তৰ ব্যাসাৰ্ধ, \(R = OA = O’B\)
\(\therefore 30 + 10\) মি= 40 মি
আৰু, \(AB = CD = EF = GH = 106\) মি
পথটোৰ ভিতৰৰ কিনাৰ সৈতে ঘূৰি থকা মুঠ দূৰত্ব
\(=CD + EF + 2 \times\) ভিতৰৰ অর্ধবৃত্তৰ পৰিধি
\(= 106 + 106 + 2 \times \frac{22}{7} \times 30\) মি
\(= 212 + \frac{1320}{7}\) মি = \(\frac{2804}{7}\) মি
পথটোৰ মুঠ ক্ষেত্ৰফল = ABCD-ৰ ক্ষেত্ৰফল + EFGH-ৰ ক্ষেত্ৰফল + 2\(\times\) বাহিৰৰ অর্ধবৃত্তৰ ক্ষেত্ৰফল – 2 \(\times\) ভিতৰৰ অর্ধবৃত্তৰ ক্ষেত্ৰফল
\(= (AB \times CD) + (EF \times GH) + 2 \times \frac{\pi}{2} (R^2 – r^2) \) মি\(^2\)
\(= (106 \times 10) + (106 \times 10) + 2 \times \frac{22}{7} \times 70 \times 10\) মি\(^2\)
\(= 2120 + \frac{22}{7} \times 70 \times 10 \) মি\(^2\)
\(= 4320 \) মি\(^2\)
9. চিত্র 12.27ত, এটা বৃত্তৰ (O কেন্দ্ৰযুক্ত) AB আৰু CD ব্যাস দুডাল পৰস্পৰ লম্ব আৰু OD হ’ল সৰু বৃত্তটোৰ ব্যাস। যদি OA = 7 চে.মি., তেন্তে আচ্ছাদিত অঞ্চলৰ কালি নিৰ্ণয় কৰা।
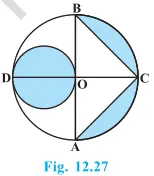
Solution:-
দিয়া আছে
ডাঙৰ বৃত্তৰ ব্যাসাৰ্ধ: \( R = 7 \, \text{cm}\)
সৰু বৃত্তৰ ব্যাসাৰ্ধ: \( r = \frac{7}{2} \, \text{cm}\)
ত্ৰিভুজ \(\triangle BCA \)-ৰ উচ্চতা OC = 7 \, \(text{cm}\)
ত্ৰিভুজ \(\triangle BCA\) -ৰ ভূমি AB = 14 , \(text{cm}\)
ত্ৰিভুজৰ ক্ষেত্ৰফল: \(\left(\frac{1}{2} \times AB \times OC = \frac{1}{2} \times 7 \times 14 = 49 \, \text{cm}^2\right)\)
ডাঙৰ বৃত্তৰ ক্ষেত্ৰফল: \(\left(\pi R^2 = \frac{22}{7} \times 7^2 = 154 \, \text{cm}^2\right)\)
ডাঙৰ অর্ধবৃত্তৰ ক্ষেত্ৰফল: \(\left(\frac{154}{2} = 77 \, \text{cm}^2\right)\)
সৰু বৃত্তৰ ক্ষেত্ৰফল: \(\left(\pi r^2 = \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} = \frac{77}{2} \, \text{cm}^2\right)\)
ৰং কৰা অঞ্চলৰ ক্ষেত্ৰফল: \(\left(\text{Area of the larger circle} – \text{Area of the triangle} – \text{Area of the larger semicircle} + \text{Area of the smaller circle}\right)\)
ৰং কৰা অঞ্চলৰ ক্ষেত্ৰফল: \(\left(154 – 49 – 77 + \frac{77}{2}\right) \, \text{cm}^2\)
\(\left(\frac{133}{2} \, \text{cm}^2 = 66.5 \, \text{cm}^2\right)\)